키워드 : mean() 함수, median() 함수, min() 함수, max() 함수, var() 함수, sd() 함수, quantile() 함수, boxplot() 함수, hist() 함수, cut() 함수, table() 함수, barplot() 함수, pie() 함수, cor() 함수, heatmap() 함수
mean() 함수 : 평균 / median() 함수 : 중앙값
min() 함수 : 최소값 / max() 함수 : 최대값
var() 함수 : 분산 / sd() 함수 : 표준편차
quantile() 함수 : 사분위수, 백분위수
boxplot() 함수 : 상자그림 / hist() 함수 : 히스토그램
cut() 함수 : 수치 데이터의 도수분포표 / table() 함수 : 범주형 데이터의 도수분포표
barplot() 함수 : 막대 그래프 / pie() 함수 : 파이 그래프
cor() 함수 : 상관계수와 상관행렬 / heatmap() 함수 : 히트맵 생성
3.1.1 데이터 대표값 탐색
문제를 분석하고 통찰력을 얻기 위해서 나무보다 숲을 먼저 봐야 하는 것처럼 빅데이터를 분석할 때도 전체적인 모습을 보고 조금씩 줌 인하여 분석할 필요가 있음.
숲을 보기 위한 방법으로 평균, 중앙값, 분산, 표준편차, 사분위수 등의 기초 통계량을 활용하거나 그래프를 통한 시각화를 활용.
방대한 양의 데이터를 한눈에 볼 수 있도록 도표나 그래프로 시각화하면 즉각적인 상황 판단에 유리, 데이터를 기억하기 쉬우며, 사람들로부터 흥미를 유발시키는 등의 장점이 있음.
이런 이유로 다양한 그래프를 활용하여 다각적인 탐색적 데이터 분석을 수행.
탐색적 자료 분석은 존 튜키라는 통계학자가 창안한 것으로 가설 검정 등에 치우친 기존 통계학을 보완한 방법론.
효과적인 분석을 위해 탐색적 데이터 분석의 목정이 가설 수립인지, 트랜드 파악인지, 변수 간의 관계 파악인지를 염두에 두고 분석하는 것이 좋음.
본격적인 데이터 분석 전에 데이터 제공처와 수집 과정의 신뢰성을 체크하는 것 또한 중요.
흔히 말하는 GIGO(Garbage In Garbage Out) 쓰레기를 넣으면 쓰레기가 나온다.
신뢰할 수 없는 데이터로 아무리 훌륭한 분석을 수행해봐야 결과를 신뢰하기 어려움.
데이터 양과 데이터 속성이 충분하지 않은 경우도 마찬가지.
그리고, 탐색적 데이터 분석 과정이 선입견 없이 객관적으로 진행되고 있는지도 주의를 기울여야 함.
이 모든 것이 신뢰성과 관련.
3.1.1.1 평균과 중앙값
평균, 중앙값 등의 대표값을 추정하는 것은 데이터 탐색의 기초 단계에 해당.
데이터 요약을 통해서 데이터의 특징, 데이터 간 차이를 파악할 수 있으며, 대부분의 값이 어디쯤 위치하는지 추정이 가능.
각 기업 연봉 데이터
> A_salary <- c(25,28,50,60,30,35,40,70,40,70,40,100,30,30)
> B_salary <- c(20,40,25,25,35,25,20,10,55,65,100,100,150,300)두 기업 직원들의 평균 연봉을 비교. mean() 평균을 구함.
> mean(A_salary)
[1] 46.28571
> mean(B_salary)
[1] 69.28571
>
> #결측값(NA)이 있는 경우 결측값을 제거하고 평균을 구할 때는 na.rm = T 인자를 사용
> mean(A_salary, na.rm = T)
[1] 46.28571평균 연봉은 B가 더 높음.
이번에는 중앙값을 비교. median()로 중앙값을 구함.
> median(A_salary)
[1] 40
> median(B_salary)
[1] 37.5
>
> median(A_salary, na.rm = T)
[1] 40중앙값은 A가 더 높음.
평균 연봉은 B가 더 높고, 중앙값은 A가 더 높음. 이렇다면 어느 기업이 연봉이 더 높다고 말할 수 있을까?
평균과 중앙값이 차이가 나는 이유는?
평균은 이상값에 매우 민감. 반면, 중앙값은 크게 달라지지 않음.
이런 이유로 평균만으로는 대표값으로 충분하지 않은 경우가 많음. 이 경우에도 B가 매우 높은 연봉 한두 건 때문에 평균이 높음.
3.1.1.2 절사평균
이상값에 민감한 평균의 특징을 보완한 것.
절사평균은 크기 순으로 정렬한 후 양끝에 일정 개수의 값을 삭제하고, 남은 값으로 구한 평균을 말함.
흔히, 체조 경기에서 사용되는 체점 방법. 특정 심판이 특정 선수에게 점수를 몰아주거나 점수를 낮추는 부정행위를 막을 수 있음.
mean() 함수에 trim 매개변수로 절사평균을 구함.
# trim으로 양끝 10%씩 제외하고 평균을 구함.
> mean(A_salary, trim = 0.1)
[1] 43.58333
> mean(B_salary, trim = 0.1)
[1] 55
3.1.1.3 가중평균
여러 모집단의 샘플이 똑같이 수집되지 않는 경우가 많음.
예를 들어, 온라인 설문조사 시, 각 나이별로 참여율이 다른 경우 이를 보정하기 위한 방법으로 데이터가 부족한 그룹에 더 높은 가중치를 적용.
이러한 용도의 평균이 가중평균
가중평균의 식. 각 데이터 $x_{i}$ 값에 가중치 $w_{i}$를 곱한 값의 총합을 가중치의 총합으로 나눔.
$$\overline{x_{n}}=\dfrac{\sum ^{n}_{i=1}W_{i}x_{i}}{\sum ^{n}_{i=1}W_{i}}$$
3.1.2 데이터 대표값 탐색
분산도(degree of dispersion)란 관측된 데이터가 흩어져 있는 정도를 말하며 이를 나타내는 방법으로는 범위, 분산, 표준편차 등이 있음.
3.1.2.1 최소값, 최대값으로 범위 탐색
범위(range)는 관측된 값들 중에서의 최대값과 최소값의 차이로 분산도를 측정하는 간단한 방법.
범위는 이해가 쉽고 계산도 편리하지만 두 극단적인 수치의 차이만 나타낼 뿐 그 극단적인 수치들 사이에서의 분포 양상은 전혀 설명을 못한다.
A, B 연봉의 범위.
# 최소 / 최대
> range(A_salary)
[1] 25 100
> range(B_salary)
[1] 10 300
최소값, 최대값을 각각 min(), max()로 구할 수 있음.
> max(A_salary)
[1] 100
> min(A_salary)
[1] 25
>
> max(B_salary)
[1] 300
> min(B_salary)
[1] 10
A 연봉의 범위는 25 ~ 100, B 연봉의 범위는 10 ~ 300.
B기업의 최소값, 최대값의 범위가 더 넓음을 알 수 있음. 하지만, 극단값만 차이가 나는 것일 수도 있기 때문에 좀 더 객관적인 편차를 확인해 보기 위해 분산과 표준편차를 구함.
3.1.2.2 분산과 표준편차
분산은 var(), 표준편차는 sd()를 이용하여 구함.
> # 분산
> var(A_salary)
[1] 464.6813
> var(B_salary)
[1] 6010.989
>
> # 표준편차
> sd(A_salary)
[1] 21.55647
> sd(B_salary)
[1] 77.53057A의 표준편차는 21.55647, B의 표준편차는 77.53057로 B기업 직원의 연봉 편차가 큰 것으로 확인.
3.1.3 데이터 분포 탐색
분산과 표준편차는 분산도를 하나의 값으로 요약하여 확인할 수 있지만 수치가 전반적으로 어떻게 분포하고 있는지를 알아보려면 다른 방법이 필요.
데이터를 정렬한 후 0%, 25%, 50%, 75%, 100% 지점의 수를 구하는 사분위수와 상자그림, 히스토그램, 도수분포표, 막대 그래프, 파이 그래프 등이 데이터 분포를 탐색하기 위해 자주 사용.
3.1.3.1 백분위수와 사분위수
백분위수 : 데이터를 정렬한 후, 특정 퍼센트 지점의 수.
0% 지점은 최소값, 100% 지점은 최대값. 50% 지점의 수는 중앙값과 같음.
상위 10% 해당되는 지점의 값을 구하고 싶으면 90% 지점의 백분위수를 구하면 됨.
quantile() 함수를 이용하여 백분위수를 구함.
> # 90% 백분위수
> quantile(A_salary, 0.9)
90%
70
> quantile(B_salary, 0.9)
90%
135
상위 10% 해당되는 연봉의 B기업이 더 높음이 확인.
백분위수 중 0%, 25%, 50%, 75%, 100%를 특별히 사분위수라고 함.
quantile() 함수를 이용하여 사분위수를 구함.
> # 사분위수
> quantile(A_salary)
0% 25% 50% 75% 100%
25.0 30.0 40.0 57.5 100.0
> quantile(B_salary)
0% 25% 50% 75% 100%
10.00 25.00 37.50 91.25 300.00이 예에서 0% 지점의 값을 비교하여 보면 최저 연봉은 A이 더 높다는 것을 알 수 있음.
50% 지점의 값을 비교하여 보면 연봉 중앙값은 A 기업이 조금 더 높다는 것을 알 수 있음.
반면에 상위 그룹의 연봉은 B가 더 높다.
3.1.3.2 상자그림(Boxplot)
앞서 본 전체 관측값 범위와 사분위수, 그리고 이상값까지 시각적으로 확인해볼 수 있는 그래프

> boxplot(A_salary,B_salary,names = c("A","B"))
두 개의 전체 번위는 얼마나 차이가 나는지, 중앙값은 얼마나 차이가 나는지 등을 수치로 확인헸을때보다 훨씬 이해하기 쉽소 직관적으로 비교.
B는 이상값 데이터가 존재하고, B기업이 A에 비해 급여의 전체 범위 및 편차가 큰 것을 알 수 있음.
최저 연봉과 연봉 중앙값은 A이 조금 더 높고, 상위 그룹의 연봉은 B가 높다는 것을 시각적으로 확인.
3.1.3.3 히스토그램
구간별 값의 분포는 히스토그램으로 시각화할 수 있음.
hist()로 히스토그램을 그림. breaks 매개인자의 숫자만큼 구간을 나누어 X축에 배치, 그 구간의 데이터 개수를 Y축의 막대 길이로 표현.
hist(A_salary, xlab = "A", ylab = "인원수", breaks = 5)
hist(B_salary, xlab = "B", ylab = "인원수", breaks = 5)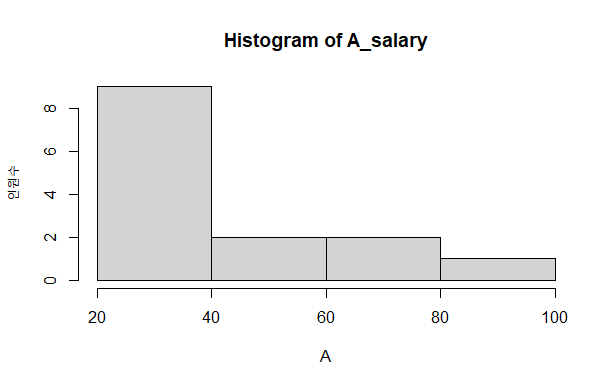
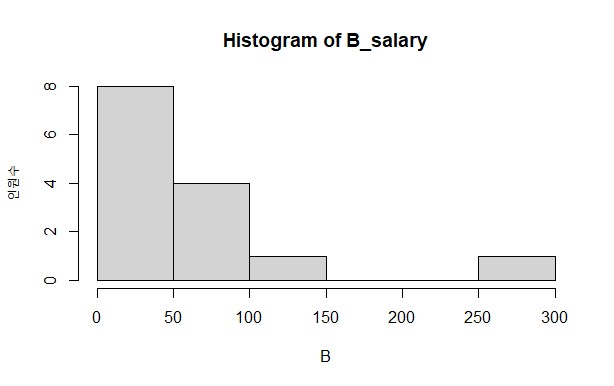
히스토그램은 데이터가 연속형 수치 데이터인 경우 데이터의 분포를 시각화하기에 좋은 그래프.
이와 유사한 그래프로 막대 그래프가 있음.
- 막대 그래프와 히스토그램의 차이점
막대 그래프 : 이산형 수치 데이터나 범주형 데이터의 경우 사용. 막대와 막대 사이를 떨어뜨려 표현.
히스토그램 : 연속형 수치 데이터의 경우 사용. 막대와 막대 사이를 붙여서 그림.
3.1.3.4 도수분포표
수집된 변수의 데이터를 범주 또는 동일한 크기의 구간으로 분류하고 각 구간마다 몇 개의 데이터가 존재하는지를 정리한 표로 많은 데이터를 알기 쉽게 정리하는 통계적인 방법 중의 하나.
데이터 특성을 요약하는 정리하는 기술 통계학에서 가장 기본적인 역할.
수치 데이터는 도수분포표를 생성할 때 cut() 함수가 유용함.
> cut_value <- cut(A_salary, breaks = 5)
> freq <- table(cut_value)
>
> freq
cut_value
(24.9,40] (40,55] (55,70] (70,85] (85,100]
9 1 3 0 1히스토그램은 이 도수분포표를 시각화하는 방법.
히스토그램을 생성하는 이전 예의 프로그램 코드에서 본 바와 같이 도수분포표를 별도로 작성하는 프로그램 코드 없이 hist()를 이용하여 바로 히스토그램을 그릴 수 있음.
범주형 데이터는 table() 함수로 편리하게 도수분포표를 생성.
> A_gender <- as.factor(c("남","남","남","남","남","남","남","남","남","여","여","여","여","여"))
> B_gender <- as.factor(c("남","남","남","남","여","여","여","여","여","여","여","남","여","여"))
> A <- data.frame(gender <- A_gender, salary <- A_salary)
> B <- data.frame(gender <- B_gender, salary <- B_salary)
> # 도수분포표를 생성
> freqA <- table(A$gender)
> freqA
남 여
9 5
>
>
> # 도수분포표를 생성
> freqB <- table(B$gender)
> freqB
남 여
5 9
한 범주에 속하는 빈도가 전체 관찰수에 비하여 어느 정도의 비중을 차지하고 있는가를 알아보는 상대적인 빈도가 유용한 경우가 있음.
prop.table()로 손쉽게 상대적 빈도표를 구할 수 있음.
> # A사의 남녀 도수분포표를 구해 저장한 freqA를 이용
> prop.table(freqA)
남 여
0.6428571 0.3571429
>
> # B사의 남녀 도수분포표를 구해 저장한 freqB를 이용
> prop.table(freqB)
남 여
0.3571429 0.6428571
3.1.3.5 막대 그래프
범주형 데이터나 이산형 수치 데이터의 도수분포표를 시각화하기 위해 막대 그래프를 사용.
barplot() 함수로 막대 그래프를 작성.
> # A사의 남녀 도수분포표를 구해 저장한 freqA를 이용
> barplot(freqA, names = c("남", "여"), col = c("skyblue","pink"), ylim = c(0,10))
> title(main = "A사")> # B사의 남녀 도수분포표를 구해 저장한 freqB를 이용
> barplot(freqB, names = c("남", "여"), col = c("skyblue","pink"), ylim = c(0,10))
> title(main = "B사")
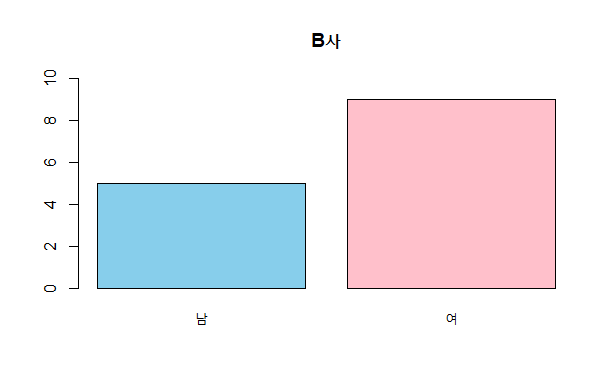
도수분포표로 각 범주별 분포를 확인할 수 있었지만 숫자로 확인하는 것보다 막대 그래프로 시각화하면 빠른 시간에 직관적으로 분포를 확인.
3.1.3.6 파이 그래프
분포의 시각화를 위해 파이 그래프를 사용.
pie(x = freqA, col = c("skyblue","pink"), main = "A사")
pie(x = freqB, col = c("skyblue","pink"), main = "B사")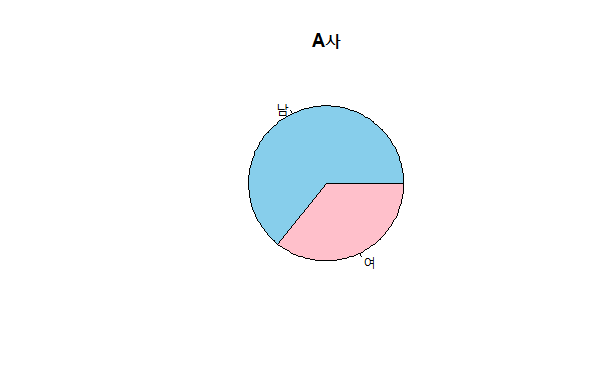
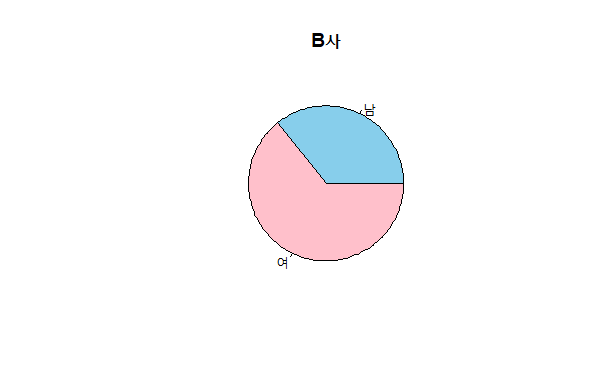
이 예와 같이 범주가 몇 개 되지 않고, 차이가 확연한 경우 파이 그래프가 유용.
하지만, 범주가 많거나, 범주별 데이터 크기의 차이가 근소한 경우는 파이 그래프로 그 차이를 확인하기 어려움.
그럴 경우 막대 그래프가 더 많이 사용.
3.1.4 변수 간 관계 탐색
변수 간의 관련성을 탐색하기 위해 산점도 그래프, 상관계수, 상관행렬, 상관행렬 히트맵 등을 이용.
3.1.4.1 산점도 그래프(scatter plot)
변수와 변수 간의 관계 시각화에 유용한 그래프.
산점도 그래프는 데이터를 X축과 Y축에 점으로 표현.
두 변수가 양의 선형적 상관관계를 가지고 있을 때 산점도 그래프는 정비례 양상을 보여줌.
두 변수가 음의 선형적 상관관계를 가지고 있을 때 산점도 그래프는 반비례 양상을 보여줌.
> A_hireyears <- c(1, 1, 5, 6, 3, 3, 4, 7, 4, 7, 4, 10, 3, 3)
> A <- data.frame(salary = A_salary, hireyears <- A_hireyears)
> # 산점도 그래프
> plot(A$hireyears, A$salary, xlab = "근무년수", ylab = "연봉")
연봉과 근무년차 산점도 그래프를 보면 대체적으로 근무년차 값이 클수록 연봉도 큰 것을 확인할 수 있음. - 양의 선형적 상관관계
pairs() 함수로 여러 가지 변수의 산점도 그래프를 한눈에 볼 수 있도록 작성할 수 있음.
다음은 아이리스(iris) 데이터프레임의 산점도 그래프 행렬 작성 예.
아이리스 데이터프레임은 R의 샘플 데이터로 아이리스 붓꽃의 꽃받침 길이(Sepal.Length), 꽃받침 너비(Sepal.Width), 꽃잎 길이(Petal.Length), 꽃잎 너비(Petal.Width), 품종(Species) 변수들의 관측 데이터가 있는데 데이터 분석을 위한 샘플 데이터로 자주 활용.
다음은 아이리스 데이터프레임의 품종(Species) 변수를 제외한 나머지 변수로 산점도 그래프 행렬을 생성.
pairs(iris[, 1:4], main = "iris data")
3.1.4.2 상관계수
변수 간의 관련성을 수치로 계산.
가장 많이 사용하는 계산법으로 피어슨 상관계수가 있음.
피어슨 상관계수는 -1에서 1사이의 값을 가짐. 피어슨 상관계수값이 1에 가까울수록 양의 상관관계고, -1에 가까울수록 음의 상관관계, 두 변수가 독립일 때 0에 가까운 수를 갖음.
cor() 함수로 상관계수를 구함.
> cor(A$hireyears,A$salary)
[1] 0.9751623A의 연봉고 근무년차 변수의 상관관계가 0.9751623. 산점도 그래프에서 추정했던 것처럼 강한 양의 상관관계가 있음.
3.1.4.3 상관행렬(Correlataion Matrix Heatmap)
여러 변수 간의 상관계수 값으로 생성한 행렬.
cor() 함수로 간단히 상관행렬을 구할 수 있음.
> # 상관행렬
> cor(iris[, 1:4])
Sepal.Length Sepal.Width Petal.Length Petal.Width
Sepal.Length 1.0000000 -0.1175698 0.8717538 0.8179411
Sepal.Width -0.1175698 1.0000000 -0.4284401 -0.3661259
Petal.Length 0.8717538 -0.4284401 1.0000000 0.9628654
Petal.Width 0.8179411 -0.3661259 0.9628654 1.0000000Petal.Length 변수와 Sepal.Length 변수의 상관계수가 0.8717538, Petal.Width 변수와 Sepal.Length 변수의 상관계수가 0.8179411, Petal.Width 변수와 Petal.Length 변수의 상관계수가 0.9628654로 강한 양의 선형적 상관관계가 있음.
3.1.4.4 상관행렬 히트맵
많은 변수로 상관행렬을 만들면 상관계수 값을 일일이 확인하기 어려움.
이 경우 상관행렬을 히트맵으로 시각화하는 것이 매우 유용.
> # 상관행렬 히트맵
> heatmap(cor(iris[, 1:4]))
'@@@ 데이터분석 > 데이터 분석의 모든 것' 카테고리의 다른 글
| Part 2. 데이터 마트와 통계 분석 (0) | 2021.10.08 |
|---|---|
| Chapter 2. R 프로그래밍 - 2.5 R을 이용한 데이터 조작 방법 (0) | 2021.10.08 |
| Chapter 2. R 프로그래밍 - 2.4 R 기초 프로그래밍 (0) | 2021.10.04 |
| Chapter 2. R 프로그래밍 - 2.3 데이터 구조 (0) | 2021.09.12 |
| Chapter 2. R 프로그래밍 - 2.2 변수와 데이터 타입 (0) | 2021.09.12 |